LoRA for Sequence Classification
Low-rank adaption, or LoRA, is another parameter-efficient fine-tuning techniques to align large models to specific tasks. The core idea is to approximate updates of a large matrix by two matrices of smaller rank:
The idea works becasue in the fine-tuning stage, the data we use is very small and narrowly-focused (on some speficic domain) compared to the pretrained data, and thus we can represent the updates with smaller matrices.
from datasets import load_dataset
from peft import get_peft_model, LoraConfig, TaskType
from transformers import AutoTokenizer, AutoModelForSequenceClassification
from transformers import Trainer, TrainingArguments
import torch
from datasets.utils.logging import disable_progress_bar
disable_progress_bar()
0. LoRA
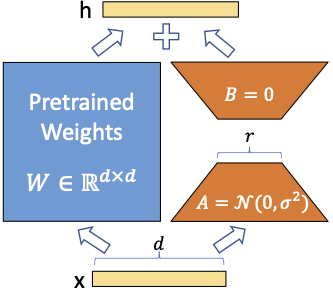
Let's say \(M\) is a \(d \times d\) matrix in a pretrained model, usually in some linear module \(x \mapsto xM\). In the traditional way to fine tune the model with labelled data, all parameters in \(M\) will be updated, and that are \(d^2\) many parameters. When \(d\) is large, say 1000, the number of parameters for \(M\) alone is already 1 million. Nowadays, pretrain models come with many large matrices and easily have billions of parameters. However, when we fine-tune model for specific task, we might have limited labelled data. We might only have thousands of samples, or even only hundreds. Comparing to the number of parameters, the number of samples is usually disportionally small. This disportinality motivates us to reduce the number of parameters in fine-tuning.
LoRA reduces the number of parameters by approximating a matrix with two smaller matrics. After fine-tuning, the matrix \(M\) will be udpated by some delta \(\Delta M\). In other words, \(M\) is updated to \(M + \Delta M\). Here \(\Delta M\) is another \(d \times d\) matrix. Since we only have a small sample set for fine-tuning compared to the pretraining stage, \(\Delta M\) is most likely not of full rank. Rank is a mathematical concept that measures the "dimension" of the matrix. In laymen terms, it represents the number of independent information the matrix carries. In pretraining, LLMs are trained on large corpus with various domains. But for a specific task, we might only want to focus on a few domains. For example, if we want to classifiy the sentiment of some financial statements, we focus on the finance and our samples should be fincial statements and their sentiments. We won't see art descriptions in this financial sentiment dataset, thus we expect \(\Delta M\) carries no art related information in the financial sentiment analysis.
Realizing the above high level observation, LoRA approximate \(\Delta M\) by two smaller matrics of rank \(r\) (\(r\) is a hyperparameter):
where \(A\) is of size \(d \times r\) and \(B\) is \(r \times d\), and \(s \in \mathbb{R}\) is some scaling hyperparameter. In implementation, the linear module \(x \mapsto xM\) will be modified to \(x \mapsto xM + s ((xA)B)\) with \(M\) frozen. So the trainable parameters become those in \(A\) and \(B\), and the trainable parameters is \(2rd\). If \(d = 1000\) and \(r\) is chosen to be \(16\), then we reduce the total number of trainable parameters \(d^2 = 1,000,000\) down to \(2rd = 32,000\). The trainable parameters are only 3.2% of the original parameters.
There are two major hyperparameters in LoRA: the rank \(r\) and the scaling factor \(s\). The rank \(r\) control how much independent information you want to extract from the labelled dataset, and \(s\) control how much you want the extracted information affect the original model. The scaling factor also comes with another form, the alpha hyperparameter \(\alpha\), in which \(s = \alpha / r\).
The procedure of fine-tuning with LoRA is made simple by the peft package. Actually, it is almost identical to my previous article Prompt Tuning for Sequence Classification. I am going to redo financial sentiment in the previous artical with LoRA so that I can resue most of the code in that article. I want to point out in advance that the major difference is in section 3 where we set the PEFTModel for LoRA.
1. Data Preparation
# load dataset
ds = load_dataset("vumichien/financial-sentiment")
labels = ["positive", "negative", "neutral"]
label2id = dict(zip(labels, range(3)))
id2label = dict(zip(range(3), labels))
# setup template
model_path = "Qwen/Qwen2.5-0.5B-Instruct"
tokenizer = AutoTokenizer.from_pretrained(
model_path,
padding_side="left",
)
user_prompt_template = """What is the sentiment of the following text related to finance?
negative, neutral or positive: {text}
Give your answer in one word."""
messages = [
{"role": "system", "content": "You are a helpful assistant."},
{"role": "user", "content": user_prompt_template}
]
prompt_template = tokenizer.apply_chat_template(
messages,
tokenize=False,
add_generation_prompt=True
)
# apply template to the dataset
def get_prompt(example):
prompt = prompt_template.format(text=example["text"])
return {"prompt": prompt}
ds = ds.map(get_prompt)
print(ds)
DatasetDict({
train: Dataset({
features: ['text', 'label_experts', 'prompt'],
num_rows: 1811
})
valid: Dataset({
features: ['text', 'label_experts', 'prompt'],
num_rows: 453
})
})
2. Setup Model
We load the LLM as a classifier. We use the corresponding token weights for the labels positive, negative and neutral to initialize the score weight.
model = AutoModelForSequenceClassification.from_pretrained(
model_path,
num_labels=len(labels),
id2label=id2label,
label2id=label2id,
torch_dtype="float32",
device_map="auto"
)
# set the pad token
model.config.pad_token = tokenizer.pad_token
model.config.pad_token_id = tokenizer.pad_token_id
# initialize the score layer for the classifier
labels_token_ids = [
tokenizer.encode(label)[0]
for label in labels
]
with torch.no_grad():
score_weight = model.model.embed_tokens.weight[labels_token_ids]
model.score.weight.copy_(score_weight)
model.model.embed_tokens.weight[tokenizer.pad_token_id] = 0.0
Some weights of Qwen2ForSequenceClassification were not initialized from the model checkpoint at Qwen/Qwen2.5-0.5B-Instruct and are newly initialized: ['score.weight'] You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.
def eval_model_on_accuracy(model, tokenizer, dataset, batch_size=32):
"""Evaluate the model's accuracy on the dataset.
The dataset is assumed to have `prompt` and `label_experts`.
"""
predicted_labels = []
prompts = dataset["prompt"]
for batch_begin in range(0, len(prompts), batch_size):
batch_end = batch_begin + batch_size
batch_texts = prompts[batch_begin: batch_end]
# tokenize batch of texts
batch_inputs = tokenizer(
batch_texts,
padding=True,
return_tensors="pt",
).to(model.device)
# scoring
with torch.no_grad():
batch_outputs = model(**batch_inputs)
# get the last predicted tokens
predicted_ids = batch_outputs.logits.argmax(-1)
for pid in predicted_ids:
predicted_labels.append(labels[pid])
correct = 0
for predicted, truth in zip(predicted_labels, dataset["label_experts"]):
correct += predicted == truth
accuracy = correct / len(dataset)
print(f"Accuracy: {accuracy:.2%}")
Get the current model performance before fine-tuning on the validation set as the baseline.
eval_model_on_accuracy(model, tokenizer, ds["valid"])
Accuracy: 78.59%
3. PEFT model for LoRA
The most important hyperparameters for LoRA are the rank \(r\) and the scaling factor \(s\). In this experiment, we set the rank to be \(8\), and alpha to be \(16\). Note that the scaling factor and alpha is related by \(s = \alpha / r\) (there are other ways to relate alpha and scaling factor), so the scaling factor in our experiment is \(2\). We can also choose what linear modules to apply LoRA with the target_modules argument. I choose to apply LoRA to linear modules in the attention modules of Qwen model.
peft_config = LoraConfig(
task_type=TaskType.SEQ_CLS,
target_modules=["q_proj", "v_proj", "k_proj", "o_proj"],
r=8,
lora_alpha=16,
lora_dropout=0.1,
bias="none",
)
peft_model = get_peft_model(model, peft_config)
peft_model.print_trainable_parameters()
trainable params: 1,084,032 || all params: 495,119,488 || trainable%: 0.2189
The number of trainable parameters is driven by the hyperparameter \(r\) and target_modules. The trainable parameters is only 0.2189% with the above configuration for the Qwen model we use.
def tokenize_dataset(example):
"""Tokenize the examples."""
prompt = example["prompt"]
inputs = tokenizer(prompt, truncation=False)
inputs["labels"] = label2id[example["label_experts"]]
return inputs
# tokenize the prompt and labels
tokenized_train = ds["train"].map(
tokenize_dataset,
remove_columns=ds["train"].column_names
)
# split the train further into train_train, train_valid for training
tokenized_train = tokenized_train.train_test_split(test_size=0.25)
tokenized_train
DatasetDict({
train: Dataset({
features: ['input_ids', 'attention_mask', 'labels'],
num_rows: 1358
})
test: Dataset({
features: ['input_ids', 'attention_mask', 'labels'],
num_rows: 453
})
})
BATCH_SIZE = 8
training_arguments = TrainingArguments(
output_dir="data/lora",
per_device_train_batch_size=BATCH_SIZE,
per_device_eval_batch_size=BATCH_SIZE,
num_train_epochs=3,
learning_rate=1e-5,
weight_decay=0.01,
eval_strategy="epoch",
save_strategy="epoch",
logging_strategy="epoch",
load_best_model_at_end=True,
)
trainer = Trainer(
model=peft_model,
processing_class=tokenizer,
args=training_arguments,
train_dataset=tokenized_train["train"],
eval_dataset=tokenized_train["test"]
)
trainer.train()
None
No label_names provided for model class `PeftModelForSequenceClassification`. Since `PeftModel` hides base models input arguments, if label_names is not given, label_names can't be set automatically within `Trainer`. Note that empty label_names list will be used instead.
<IPython.core.display.HTML object>
| Epoch | Training Loss | Validation Loss |
|---|---|---|
| 1 | 0.305500 | 0.195282 |
| 2 | 0.202700 | 0.165687 |
| 3 | 0.183300 | 0.160726 |
eval_model_on_accuracy(peft_model, tokenizer, ds["valid"])
Accuracy: 94.92%For a comparison of performance, the zero shot learning has accuracy 78.5% on the validation set. Prompt tuning can achieve 93.1% in accuracy, see my previous article if interested. And LoRA is even better at 94.9% accuracy. This is not a surprise given that LoRA actually has more trainable parameters (about 50x) than that in prompt tuning.