[npnet] 优化器
这篇笔记尝试着实现几种简单的机遇梯度下降的优化器 (Optimizer)。主要的参考资料是 Neural Networks Part 3: Learning and Evaluation。另外我还参考了 An overview of gradient descent optimization algorithms。这篇博文不仅有篇对应的论文:An overview of gradient descent optimization algorithms,还已经被翻译成中文了:梯度下降优化算法综述。
import numpy as np
import matplotlib.pyplot as plt
%run import_npnet.py
npnet = import_npnet(3)
重新设计优化器
我们之前在本系列关于线性回归的笔记中定义了简单的优化器基类 (base class),并且继承此基类定义了梯度下降 SGD。为了更方便地实现其他优化器,我将 Optimizer.step 分化成三步:正则 (regularization),计算参数更新,以及进行参数更新。其中正则以及参数更新是所有优化器共同的功能,所以都在基类中实现了,子类只要实现 Optimizer.get_updates 去定义如何计算参数的更新量。
基类对参数的正则使用了 L2 正则。假设正则参数为 \(\alpha\),L2 正则是指在计算损失的时候加上
其中 \(|w|_2\) 是所有参数 \(w\) 的 L2 范式 (norm)。在我们的实现中,参数的 L2 范式并没有真正加到损失中,而是隐式地对参数的偏导数增加了 \(\alpha w\)。
# import
class Optimizer:
def __init__(self, model, lr=1e-3, weight_decay=0.0, **kwargs):
self.model = model
self.parameters = model._parameters
self.gradients = model._gradients
self.lr = lr
self.weight_decay = weight_decay
self.updates = [
{
key: np.zeros_like(val)
for key, val in params.items()
}
for params in self.parameters
]
def clear(self):
self.updates = [
{
key: np.zeros_like(val)
for key, val in params.items()
}
for params in self.parameters
]
for attr in dir(self):
if not attr.startswith('caches'):
continue
val = getattr(self, attr)
if not isinstance(val, list) or \
not all(isinstance(item, dict) for item in val):
continue
for cache in val:
for key in cache:
cache[key] = np.zeros_like(cache[key])
def step(self):
self.regularize()
self.get_updates()
for params, updates in zip(self.parameters, self.updates):
for name in params.keys():
params[name] += updates[name]
def get_updates(self):
raise NotImplementedError()
def regularize(self):
weight_decay = self.weight_decay
if weight_decay == 0.0:
return
for params, grads in zip(self.parameters, self.gradients):
for name in params.keys():
grads[name] += weight_decay * params[name]
def zero_grad(self):
for grads in self.gradients:
for g in grads.values():
g.fill(0.0)
def __repr__(self):
return f"<{self.__class__.__name__}>"
如果我们想使用其他正则方法,比如 L1 正则,我们无须重新定义基类以及所有子类,而可以通过 Python 的方法解析顺序 (method resoltuion order) 达到修改的目的。比如我们可以定义一个 Optimizer 的子类 L1Optimizer,然后在 L1Optimizer.regularize 中实现 L1 正则。
# import
class L1Optimizer(Optimizer):
def regularize(self):
weight_decay = self.weight_decay
if weight_decay == 0.0:
return
for params, grads in zip(self.parameters, self.gradients):
for name in params.keys():
grads[name] += weight_decay * np.sign(params[name])
假设我们已经实现了基于 Optimizer 的梯度下降 SGD,我们只需使用如下代码实现使用 L1 正则的 L1SGD:
class L1SGD(L1Optimizer, SGD):
pass
(注意:上述两行代码在 Markdown Cell 中,不在 Code Cell 中。)
动量法
我们用 \(w\) 代表参数,而用损失函数 \(L(w)\) 代表参数为 \(w\) 时模型的损失。训练模型的目标是找到 \(w^\ast\) 使得损失函数 \(L(w^\ast)\) 达到最小值。梯度下降法是随机从一个参数 \(w_0\) 出发,然后根据使用迭代公式
不断逼近最优参数 \(w^\ast\)。这里的 \(v_t\) 代表在第 \(t\) 次迭代时参数的更新量,而 \(\lambda\) 是我们选定的学习率 (learning rate)。
按照参考资料 Neural Networks Part 3: Learning and Evaluation 的说法,动量法源于优化问题物理的角度。我们将损失函数 \(L\) 想象成群山,\(w\)代表的是高度,寻找最优参数 \(w^\ast\) 相当于寻找群山最低点的高度。上面公式中的 \(v_t\) 代表了 \(t\) 时刻的速度。我们随机从一个地方 \(w_0\) 出发,初始速度为 \(v_0 = 0\)。在 \(t\) 时刻,\(-\lambda \, \nabla_w L(w_{t-1})\) 给出的是速度的变化量,而并不是速度本身,真正的速度应该 \(v_{t-1} -\lambda \, \nabla_w L(w_{t-1})\)。考虑到摩擦力,我们引进一个超参数 \(\mu \in [0, 1]\):
超参数 \(\mu\) 被称作动量参数 (momentum),但事实上它跟动量没有关系,而是来自于摩擦系数。在动量法中如果一个方向的速度增量没有改变方向,那么这个方向上的速度会越来越大。
Nesterov 动量法
Nesterov 动量法的主要思想是:在时刻 \(t\),如果没有速度的变化量 \(-\lambda \, \nabla_w L(w_{t-1})\),那么下一个 \(w\) 应该在的地方是 \(w_{t-1} + \mu v_{t-1}\),我们用 \(-\lambda \, \nabla_w L(w_{t-1} + \mu v_{t-1})\) 来代替速度的变化量。这样我们的迭代公式就变成了:
让我借用参考资料 Neural Networks Part 3: Learning and Evaluation 的一张图来解释动量法以及 Nesterov 动量法的区别:
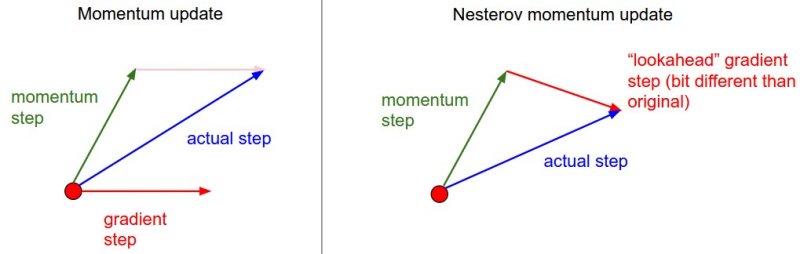
动量法的梯度以及动量都是在同一个点计算的,而 Nesterov 动量法的梯度在动量后一步算的。Nesterov 的迭代公式有个实现的难点:梯度是在 \(w_{t-1} + \mu v_{t-1}\) 这个点计算的,但是我们模型的偏导数是对上一个参数 \(w_{t-1}\) 求的。为了避免算两次偏导数,我们将参数变成 \(\theta_t = w_t + \mu v_t\),那么 Nesterov 的迭代公式等价于
以上公式就不会计算两次偏导数了。虽然 \(\theta_t\) 不等于 \(w_t\),但是两者只相差一个 \(\mu v_t\),权当算作最后一次迭代后又做了一次额外的更新了。所以我们在实现中就将 \(\theta_t\) 与 \(w_t\) 等同了。我们注意到当 \(\mu = 0\) 时迭代公式退化成一般的梯度下降了。我们将动量法和 Nesterov 动量法都实现在新的梯度下降 SGD 中。
# import
class SGD(Optimizer):
def __init__(self, model, lr=1e-3, momentum=0.0,
weight_decay=0.0, nesterov=False, **kwargs):
super().__init__(model=model, lr=lr, momentum=momentum,
weight_decay=weight_decay, nesterov=nesterov, **kwargs)
self.momentum = momentum
self.nesterov = nesterov
if momentum == 0.0 and nesterov:
print('Nesterov momentum is ignored.')
nesterov = False
# 动量缓存
self.caches = [
{
key: np.zeros_like(val)
for key, val in grads.items()
}
for grads in self.gradients
]
def get_updates(self):
momentum = self.momentum
lr = self.lr
pre_caches = self.caches
caches = [
{
key: -lr * val
for key, val in grads.items()
}
for grads in self.gradients
]
if momentum != 0.0:
for vects, pre_vects in zip(caches, pre_caches):
for key in vects.keys():
vects[key] += momentum * pre_vects[key]
self.caches = caches
if not self.nesterov:
self.updates = caches
else:
self.updates = [
{
key: (1+momentum) * vects[key] - momentum * pre_vects[key]
for key in vects.keys()
}
for vects, pre_vects in zip(caches, pre_caches)
]
学习率自适应
动量法中的学习率 \(\lambda\) 是所有参数的学习率,但是选择一个适合所有参数的学习率是一件几乎不可能的事情。于是研究人员想出了很多学习率自适应的梯度下降法。我们将要实现三种此类优化器:Adagrad,RMSprop 和 Adam。在介绍它们之前我们需要定义一种矩阵按位乘法运算 \(\odot\)。给定两个大小一样的矩阵 \(A\) 和 \(B\),我们定义按位乘法的结果 \(C = A \odot B\):
如果没有特别说明,将一个函数 \(f\) 应用在一个矩阵 \(A\) 上,代表对矩阵 \(A\) 的每一位应用函数 \(f\)。
我们回忆一下我们使用过的符号:\(w\) 指模型参数,\(L\) 是损失函数,\(\nabla_w L\) 是损失函数对参数的偏导数,\(\lambda\) 是学习率。
Adagrad
Adagrad 是 Adaptive gradient 的缩写。它给出的迭代公式为
\(\epsilon\) 是一个很小的值,一般取 \(10^{-8}\),用来防止分母为0。
# import
class Adagrad(Optimizer):
def __init__(self, model, lr=1e-3, eps=1e-8, weight_decay=0.0, **kwargs):
super().__init__(model=model, lr=lr, eps=eps,
weight_decay=weight_decay, **kwargs)
self.eps = eps
# 缓存偏导数的平方
self.caches = [
{
key: np.zeros_like(val)
for key, val in grads.items()
}
for grads in self.gradients
]
def get_updates(self):
lr, eps = self.lr, self.eps
packets = zip(self.gradients, self.caches, self.updates)
for grads, caches, updates in packets:
for key in grads.keys():
caches[key] += grads[key] ** 2
updates[key] = -lr * grads[key] / np.sqrt(caches[key] + eps)
RMSprop
Adagrad 的缺点在于 \(v_t\) 是不断变大导致每次参数更新的量都在减小。RMSprop 在 \(v_t\) 的公式中引入了衰减率 \(\delta\) (decay rate) 来克服这个缺点。
\(\delta\) 一般取 \(0.9\)。
# import
class RMSprop(Optimizer):
def __init__(self, model, lr=1e-3, decay_rate=0.9, eps=1e-8,
weight_decay=0.0, **kwargs):
super().__init__(model=model, lr=lr, decay_rate=decay_rate,
eps=eps, weight_decay=weight_decay, **kwargs)
self.decay_rate = decay_rate
self.eps = eps
# 缓存偏导数的平方:v
self.caches = [
{
key: np.zeros_like(val)
for key, val in grads.items()
}
for grads in self.gradients
]
def get_updates(self):
lr, dr, eps = self.lr, self.decay_rate, self.eps
packets = zip(self.gradients, self.caches, self.updates)
for grads, caches, updates in packets:
for key in grads.keys():
caches[key] *= dr
caches[key] += (1-dr) * grads[key] ** 2
updates[key] = -lr * grads[key] / np.sqrt(caches[key] + eps)
Adam
Adam (Adaptive Moment Estimation) 是尝试结合 Adagrad 以及 RMSprop 的优势而得到的优化器。简化版的迭代公式是
一般来说,超参数 \(\beta_1=0.9, \beta_2=0.99\)。
# import
class Adam(Optimizer):
def __init__(self, model, lr=1e-3, beta1=0.9, beta2=0.99, eps=1e-8,
weight_decay=0.0, **kwargs):
super().__init__(model=model, lr=lr, beta1=beta1, beta2=beta2,
eps=eps, weight_decay=weight_decay, **kwargs)
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
# 缓存偏导数:m
self.caches1 = [
{
key: np.zeros_like(val)
for key, val in grads.items()
}
for grads in self.gradients
]
# 缓存偏导数的平方:v
self.caches2 = [
{
key: np.zeros_like(val)
for key, val in grads.items()
}
for grads in self.gradients
]
def get_updates(self):
lr, b1, b2, eps = self.lr, self.beta1, self.beta2, self.eps
packets = zip(self.gradients, self.caches1, self.caches2, self.updates)
for grads, caches1, caches2, updates in packets:
for key in grads.keys():
caches1[key] *= b1
caches1[key] += (1-b1) * grads[key]
caches2[key] *= b2
caches2[key] += (1-b2) * grads[key] ** 2
updates[key] = -lr * caches1[key] / np.sqrt(caches2[key] + eps)
优化器的比较
最后我们用上一篇笔记 Fashion MNIST 的线性模型来测试一下各种优化器的收敛速度。每个优化器最重要的参数是学习率,虽然学习率自适应的优化器对学习率的依赖没有 SGD 那么高,但是不一样的学习率对收敛性还是会有影响的。因此我们在比较优化器的时候应该为各个优化器选择一个好的学习率。比如 Adagrad 的缺点要求我们给它选择一个稍大的学习率。
images, labels = npnet.load_fashion_mnist(kind='train')
batch_size = 100
epoch = 25
criterion = npnet.CrossEntropy()
args = [
dict(cls=SGD, lr=1e-5, label='SGD'),
dict(cls=SGD, lr=1e-4, momentum=0.9, label='Momentum'),
dict(cls=SGD, lr=1e-5, momentum=0.9, nesterov=True, label='Nesterov'),
dict(cls=Adagrad, lr=1e-2, label='Adagrad'),
dict(cls=RMSprop, lr=1e-4, label='RMSprop'),
dict(cls=Adam, lr=1e-4, label='Adam')
]
为了保证公平性,我们固定一个初始模型,然后用不同的优化器训练这个模型。
lin = npnet.Linear(784, 10)
def copy_model():
model = npnet.Linear(784, 10)
for key in model.parameters:
model.parameters[key] = np.copy(lin.parameters[key])
return model
plt.figure(figsize=(15,10))
for arg in args:
model = copy_model()
optim = arg['cls'](model, **arg)
loss, *_ = npnet.train_fashion_mnist(
model=model, criterion=criterion, optim=optim,
train_images=images, train_labels=labels,
profile=True, batch_size=batch_size, epoch=epoch
)
plt.plot(np.arange(len(loss)), loss, label=arg['label'])
plt.legend()
plt.xticks(range(0, epoch+1, 5))
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('Comparision of optimizers')
plt.show()
npnet:12: RuntimeWarning: divide by zero encountered in log
从结果来看,每一种改进的优化器都比一般的 SGD 收敛得快。在这个例子中,除了 SGD 外的其他优化器在这个例子的表现都差不多,最好的是 Nesterov 动量法。我们在训练一个模型的时候都应该如这个例子般用小规模的数据先比较各种优化器的收敛速度,从而选出最合适的优化器。换言而之,我们可以将优化器当作一个超参数。
