Cassini Ovals | 叶某人的碎碎念

This post is my note for What is seminar on Cassini Ovals.

Definition

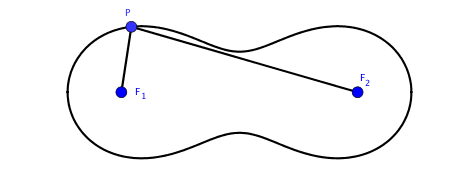
An ellipse is a geometric object formed by locus of points which have fixed sum of distances to two fixes foci.

Ellipse

In the above figure, we can express the definition of ellipses in one simple equation:

$$|PF_1|+|PF_2|=c,$$

for some $c>0$. What if we change the addition in the above equation to multiplication? This comes the definition of Cassini ovals.

Definition. A Cassini oval is a locus of points $P$ which satisfying $$|PF_1| \cdot |PF_2| = c^2,$$ for two fixed foci $F_1$ and $F_2$, and some $c > 0$.

Cassini Oval

Parametrization

If we assume that $F_1$ has coordinate $(-d, 0)$ and $F_2$ has coordinate $(d, 0)$, then points $P(x, y)$ on Cassini oval satisfy the following equation:

$$\begin{equation} \left((x-d)^2+y^2\right)\left((x+d)^2+y^2\right) = c^4. \label{20170629-1} \end{equation}$$

Equation $\eqref{20170629-1}$ is an implicit description of a Cassini oval. To get a parametric description, we will use polar system:

$$\begin{equation*} \left\{\begin{array}{l} x = r \cos \theta \\ y = r \sin \theta \end{array}\right.. \end{equation*}$$

Substituting it in $\eqref{20170629-1}$, we get

$$\begin{equation} r^4 - 2d^2 \cos(2\theta) r^2 + d^4 - c^4 = 0. \label{20170629-2} \end{equation}$$

Solving $\eqref{20170629-2}$,

$$\begin{equation*} r^2 = d^2\left(\cos(2\theta) \pm \sqrt{\left(\frac{c}{d}\right)^4-\sin^2(2\theta)}\right). \end{equation*}$$

Therefore, without specifying the range of $\theta$, we have

$$\begin{equation} r(\theta) = \pm d\sqrt{\cos(2\theta) \pm \sqrt{\left(\frac{c}{d}\right)^4-\sin^2(2\theta)}}. \label{20170629-3} \end{equation}$$

Let

$$\begin{equation*} r_+(\theta) = d\sqrt{\cos(2\theta) + \sqrt{\left(\frac{c}{d}\right)^4-\sin^2(2\theta)}}, \end{equation*}$$

and

$$\begin{equation*} r_-(\theta) = d\sqrt{\cos(2\theta) - \sqrt{\left(\frac{c}{d}\right)^4-\sin^2(2\theta)}}. \end{equation*}$$

The claim is that $r_+(\theta)$ and $r_-(\theta)$ are enough to cover all solutions in $\eqref{20170629-3}$. This is an easy consequence of the fact that $(r, \theta)$ and $(-r, \theta+\pi)$ represent a same point. The range of $\theta$ depends on the relative sizes of $c$ and $d$. And indeed, their relative sizes control the shapes of Cassini ovals.

Shape

According to $\eqref{20170629-1}$, if $(x, y)$ is on a Cassini oval, then $(x, -y), (-x, y)$ and $(-x, -y)$ are all on the Cassini oval. This is amount to say, Cassini ovals are symmetry with respect to $x$-axis and $y$-axis. To calculate $y$-intercepts of a Cassini oval, we set $x=0$ in $\eqref{20170629-1}$:

$$d^2+y^2=c^2,$$

$$y = \pm \sqrt{c^2-d^2}.$$

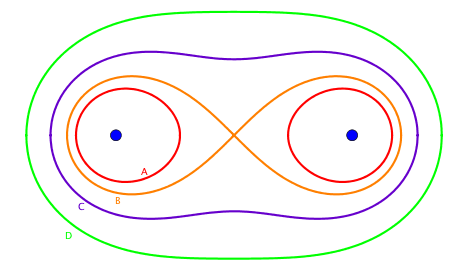
Case A: $c < d$. In this case, there is no $y$-intercepts. Such a Cassini oval consists of two cycles symmetric with respect to $y$-axis. See the red Cassini oval in the below figure.

Case B: $c = d$. There is exactly one $y$-intercept at the origin. See the orange Cassini oval below.

Case C: $d < c < \sqrt{2}d$. There are two $y$-intercepts. See the purple Cassini oval below.

Case D: $c \ge \sqrt{2}d$. There are two $y$-intercepts. See the green Cassini oval below.

Cassini Ovals

To understand the difference of the shapes between Case C and Case D, we are going to do a bit of analysis around positive $y$-intercept. Apply implicit differentiation to $\eqref{20170629-1}$, we get at $(0, y=\sqrt{c^2 - d^2})$

$$\frac{dy}{dx} = -\frac{x(x^2+c^2-2d^2)}{y(x^2+y^2+d^2)}.$$

If as in Case C, $d < c < \sqrt{2}d$, $y^\prime(x)$ is positive for small $x > 0$ and negative for small $x < 0$. Therefore, Cassini ovals in Case C have local minimums at the positive $y$-intercepts. On the contrary, Cassini ovals in Case D have local maximums at the positive $y$-intercepts.

what is note